Cubic Bezier Curve 일반식
프로그래밍/TrueType Font 2009. 6. 30. 00:26 |3차 베지어 커브 일반식 유도
혹자는 왜 하필이면 3차 베지어 커브이냐 ... 라고 궁금증을 가질 수도 있지만,
대부분의 폰트는 3차 이하의 베지어 커브들로 구성된다는 점,
3차 베지어 커브이면 원에 가까이 근사할 수 있다는 점 등이 그 이유일 것이다.
실제로 베지어 커브로는 완벽한 원을 만들 수 없다.
따지고 보면 1차 베지어 커브(사실은 직선)로도 원하는 모양을 만들 수 있긴 하다.
물론 이건 매우 비효율적이다. 어차피 픽셀로 표현되는 컴퓨터 나라에서 곡선이란 게 무의미 할 수도 있다.
아무튼 그건 그거고 ...
3차 베지어 커브의 일반식을 유도하기 위한 조건은 다음과 같다.
1. 컨트롤 포인트는 4개이다. (P0, P1, P2 and P3)
2. 곡선은 첫번째 포인트와 마지막 포인트를 지난다.
3. 곡선의 첫 지점에서의 기울기는 P0 과 P1 을 이은 직선의 기울기의 3배이다.
4. 곡선의 마지막 지점에서의 기울기는 P2 와 P3 을 이은 직선의 기울기의 3배이다.
위 사실에 근거하여,
3차 식을 다음과 같이 u에 대한 3차 식으로 두고,
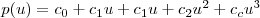
이놈을 매트릭스로 표현하면,
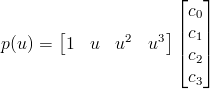
즉,
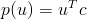
그리고 미분한 식은 다음과 같다.
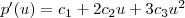
위 조건 1,2,3,4 를 적용하여 보면,
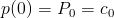
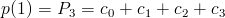
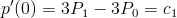
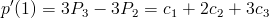
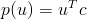 이 식에서
이 식에서
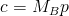 로 치환하면, 다음과 같다.
로 치환하면, 다음과 같다.
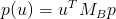
조건 1,2,3,4 로부터 유도된 식으로부터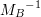
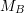 를 구할 수 있고, 값은 다음과 같다.
를 구할 수 있고, 값은 다음과 같다.
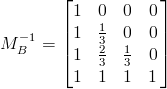

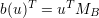 라고 치환하면,
라고 치환하면,
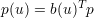 이렇게 되고,
이렇게 되고,
고로,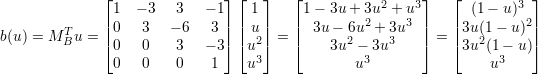 다음을 통해서 b(u) 를 구할 수 있다.
다음을 통해서 b(u) 를 구할 수 있다.
이제 다 끝났다.
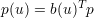
이었으므로, 다음과 같은 일반항이 도출된다.
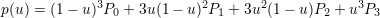
references :
http://en.wikipedia.org/wiki/B%C3%A9zier_curve
Interactive Computer Graphics 2nd Edition (Addison Wesley) p434-436
수식 편집 :
http://www.codecogs.com/
아놔 심플 ~ 수학 공식 쓰기 캐노가다 ㅜㅜ
혹자는 왜 하필이면 3차 베지어 커브이냐 ... 라고 궁금증을 가질 수도 있지만,
대부분의 폰트는 3차 이하의 베지어 커브들로 구성된다는 점,
3차 베지어 커브이면 원에 가까이 근사할 수 있다는 점 등이 그 이유일 것이다.
실제로 베지어 커브로는 완벽한 원을 만들 수 없다.
따지고 보면 1차 베지어 커브(사실은 직선)로도 원하는 모양을 만들 수 있긴 하다.
물론 이건 매우 비효율적이다. 어차피 픽셀로 표현되는 컴퓨터 나라에서 곡선이란 게 무의미 할 수도 있다.
아무튼 그건 그거고 ...
3차 베지어 커브의 일반식을 유도하기 위한 조건은 다음과 같다.
1. 컨트롤 포인트는 4개이다. (P0, P1, P2 and P3)
2. 곡선은 첫번째 포인트와 마지막 포인트를 지난다.
3. 곡선의 첫 지점에서의 기울기는 P0 과 P1 을 이은 직선의 기울기의 3배이다.
4. 곡선의 마지막 지점에서의 기울기는 P2 와 P3 을 이은 직선의 기울기의 3배이다.
위 사실에 근거하여,
3차 식을 다음과 같이 u에 대한 3차 식으로 두고,
이놈을 매트릭스로 표현하면,
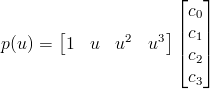
즉,
그리고 미분한 식은 다음과 같다.
위 조건 1,2,3,4 를 적용하여 보면,
조건 1,2,3,4 로부터 유도된 식으로부터
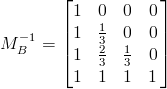

고로,
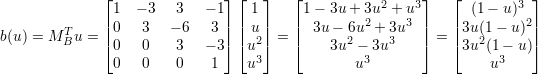
이제 다 끝났다.
이었으므로, 다음과 같은 일반항이 도출된다.
references :
http://en.wikipedia.org/wiki/B%C3%A9zier_curve
Interactive Computer Graphics 2nd Edition (Addison Wesley) p434-436
수식 편집 :
http://www.codecogs.com/
아놔 심플 ~ 수학 공식 쓰기 캐노가다 ㅜㅜ
