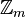Modular multiplicative inverse

references :

https://en.wikipedia.org/wiki/Modular_multiplicative_inverse

 

 

In modular arithmetic, the modular multiplicative inverse of an integer a modulo m is an integer x such that

 

That is, it is the multiplicative inverse in the ring of integers modulo m, denoted .

Once defined, x may be noted , where the fact that the inversion is m-modular is implicit.

The multiplicative inverse of a modulo m exists if and only if a and m are coprime (i.e., if gcd(a, m) = 1).^[1] If the modular multiplicative inverse of a modulo m exists, the operation of divisionby a modulo m can be defined as multiplying by the inverse, which is in essence the same concept as division in the field of reals.

[wiki]

 

 

example : 

http://codeforces.com/contest/560/problem/E

 

test code : 

are each number of factorial series and 10e9+7 coprime ?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

#include <cstdio> using namespace std; const int MOD = 1000000007; int fact[100001]; // 10e5 void make_factorial_series() {     fact[0] = fact[1] = 1;     for (int i = 2; i <= 100000; i++) {         fact[i] = (int)((long long)fact[i-1] * i % MOD);     } } int gcd(int a, int b) {     return b ? gcd(b, a%b) : a; } int main() {     make_factorial_series();     for (int i = 2; i <= 100000; i++) {         int _gcd = gcd(fact[i], MOD);         printf("%d %d ==> gcd(%d) - %s\n", fact[i], MOD, _gcd, (_gcd == 1) ? "o" : "X");     }     return 0; }

 

 

 

 

extended Euclidean algorithm

The modular multiplicative inverse of a modulo m can be found with the extended Euclidean algorithm.

The algorithm finds solutions to Bézout's identity

 

한국어: https://medium.com/@jongukim/extended-euclidean-algorithm-8101bafb9164

 

 

test codes:

#include <iostream> using namespace std; void cal(int quotient , int &r, int &new_r) {     int temp(r);     r = new_r;     new_r = temp - quotient * new_r; } int inverse(int a, int m) {     int t(0), new_t(1), r(m), new_r(a);     while (new_r) {         int quotient = r / new_r;         cal(quotient, t, new_t);         cal(quotient, r, new_r);     }     if (r > 1) return -1; // something wrong     if (t < 0) t = t + m;     return t; } int main() {     while (true) {         int a, b;         cin >> a >> b;         if (a == 0) break;         cout << inverse(a, b) << endl;     }     return 0; }